What is the connection between Suction Specific Speed and Minimum Flow?

The connection between suction specific speed S_ω (N_SS) and minimum flow (Q_min) is that, in general, a higher value of S_ω (N_SS) is associated with a higher value of Q_min.  Beyond that generalized statement, however, there is wide range of deviation and exception.

For rotodynamic (centrifugal, mixed-flow and axial flow) pumps suction specific speed is the main suction performance parameter.  As a refresher, the two commonly used equations for S_ω and N_SS are as follows.

The non-dimensional version – the one that ideally we would all be using – is:

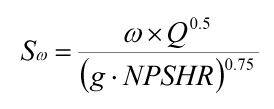
The customary version – the one with various unit conventions in use – is:

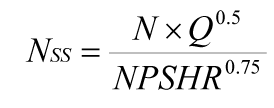
In the above equations, Q is the flow per eye of the first stage impeller.  The equation for S_ω requires consistent units and the resulting value is dimensionless.  The equation for N_SS is based on customary units and its resulting value is not strictly dimensionless, but is used as an index of suction performance capability.

The minimum flow value is not strictly defined by a single equation.  From a vibration standpoint, minimum flow may be evaluated as the product of the onset of suction recirculation (Q_SR), and factors for speed and flow (K₁), specific gravity (K₂), NPSH margin ratio (K₃), intermittency of operation (K₄) and mechanical design margin (K₅).  The equation [1] is:

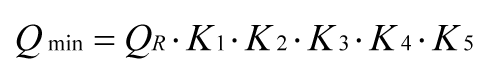
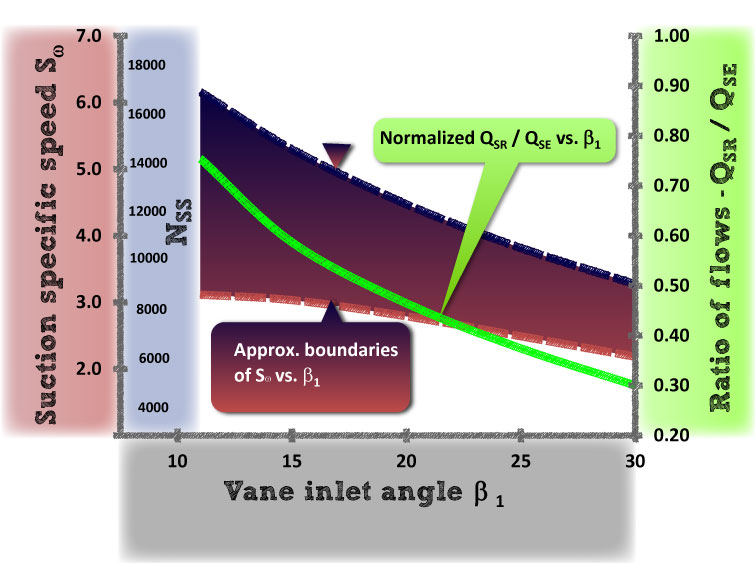
The onset of suction recirculation (Q_SR) is approximated by the product of rotational frequency (ω), impeller eye diameter (D₁), and eye and vane geometry factors, including the inlet vane angle (β₁).  The linkage between Q_SR and S_ω is inlet vane angle β₁ as detailed in reference [1].  Chart A graphically shows this connection.  Q_SR tends to increase with increasing S_ω (N_SS) or decreasing β₁.  A wide range of suction specific speeds is possible for a given impeller vane inlet angle.  The range of variation in the theoretical curve for the ratio of Q_SR/Q_SE (where the Q_SE in the denominator is the shockless entry flow) is difficult to forecast due to inlet and impeller suction geometry details which cannot be readily included in one-dimensional equations.

The factors representing pump hydraulic forces are K₁ and K₂.  These forces are roughly proportional to the product of rotational speed (N), flow (Q) and specific gravity (SG).  The speed of a given machine and its size in terms of volume rate of flow are prominent factors in establishing the severity and range of minimum flow operation.

Take, for instance, a nominal 2 x 1.5 ANSI (ASME B73.1) pump at 3500 rpm with a relatively high suction specific speed of 5.1 (14,000 US).  The minimum continuous flow is relatively low, 20% of best efficiency point flow (Q_BEP) flow pumping cold water.  In this case, a high S_ω (N_SS) and a correspondingly high value for Q_SR is offset by a low value for the product of factors K₁ and K₂ representing hydraulic forces.

A high pressure 8 x 10 boiler feed pump operating at 5500 rpm with a moderate suction specific speed of 3.2 (8,800 US) has a minimum flow of 55% of Q_BEP, pumping hot boiler feed water.  Large high energy pumps tend to require higher minimum flow limits primarily due to the effects of size and speed.

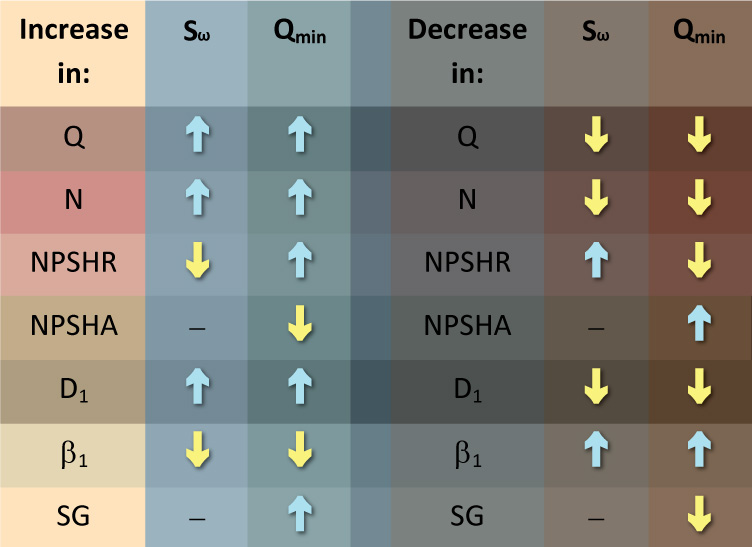
The general trends of increasing or decreasing values of key variables in relationship to S_ω (N_SS) and Q_min is shown in Table A.  Note that the effects on S_ω (N_SS) and Q_min due to a change in NPSHR are opposite.  A reduced level of NPSHR for a given NPSHA will increase the NPSH margin ratio, tending to suppress cavitation.  This reinforces the notion that S_ω (N_SS) and Q_min are substantially independent.

For some multi-stage pump applications involving a relatively low value of the NPSH margin ratio, minimum flow is governed by temperature rise to avoid flashing in the balance line return to suction.  In this case minimum flow is determined by factors other than suction specific speed.  And there are other factors for specific pumping applications that can affect minimum flow, one being the rate of cavitation erosion damage.

In summary, while suction specific speed S_ω (N_SS) can be related to the onset of suction recirculation flow Q_SR, the linkage to a practical value for minimum continuous flow Q_min requires additional factors.  A principal factor affecting minimum continuous flow, for vibration purposes, is the energy level of the machine, but other factors such as the NPSH margin ratio are important.

For an independent evaluation of factors affecting pump operation at off-peak conditions, contact an experienced consulting engineer who can help with your specific application.

[1]  S. Gopalakrishnan’s paper titled, “A New Method for Computing Minimum Flow,” Proceedings of the Fifth International Pump Users Symposium; Texas A&M University, May 1988, pp. 41-47.